[Day 22] Unsupervised Machine Learning Type 5 – ICA (Independent Component Analysis) (with a Small Python Project)
Ever wish you could untangle mixed signals like brainwaves or audio streams? ICA does just that—like magic for messy data! 🎧🧠
![[Day 22] Unsupervised Machine Learning Type 5 – ICA (Independent Component Analysis) (with a Small Python Project)](/content/images/size/w2000/2025/03/ICA.svg)
🎯 What is ICA?
Independent Component Analysis (ICA) is an unsupervised learning technique used to separate a multivariate signal into additive, statistically independent components.
While PCA focuses on uncorrelated directions that explain variance, ICA goes further — it uncovers truly independent signals hidden inside the data.
Imagine several radio stations playing at once, and you receive a single mixed audio stream. ICA is the algorithm that can pull out each radio station separately, just by analyzing the mixture — no prior knowledge needed!
You’re at a noisy party. Multiple people are talking at once. Your brain somehow focuses on one person’s voice and filters the rest. That’s what ICA does — separates mixed signals into original, independent sources.
🧩 Intuition Behind ICA
Every observation in your dataset may be a combination of multiple sources. ICA assumes:
- These sources are independent (not just uncorrelated)
- The mixing is linear
- The observed dataset is just a mixture of hidden, original signals
ICA tries to unmix the observed data to recover those independent sources.
Why ICA Is Useful
- Extracts hidden independent features from observed data.
- Helps denoise and understand signal sources.
- Great for feature extraction, compression, and signal processing.
- Often used before classification or clustering to clean and simplify complex inputs.

🌍 Real-World Use Cases of ICA
🗣️ 1. Cocktail Party Problem (Audio Source Separation)
- Multiple people speak at once in a room.
- Microphones capture overlapping sounds.
- ICA helps extract individual voices from the mix.
🧠 2. Brain Signal Analysis (EEG/MEG)
- Brain activity recorded via electrodes is noisy.
- ICA separates actual brain signals from muscle movement, eye blinks, and noise.
📡 3. Telecommunications
- Multiple data signals are transmitted simultaneously.
- ICA helps receivers separate mixed signals for clearer decoding.
🧬 4. Genomics and Imaging
are
- Complex biological datasets with overlapping gene expressions or patterns.
- ICA isolates underlying biological signals for better interpretation.
🧪 Python Project: Signal Separation with ICA
🏷 Project Name: SignalSplit – Unmixing Independent Sources Using ICA
📘 Project Context:
Imagine you're working in bio-signal processing at a health-tech company. You're given mixed data from 6 sensors — each signal is a mixture of:
- Brain waves
- Muscle movement
- Environmental noise
- Other latent sources
You apply ICA to recover each independent source — helping doctors analyze real brain patterns more accurately.
🧾 Full ICA Dataset (20 Samples × 6 Mixed Signals)
| Sample | Signal_1 | Signal_2 | Signal_3 | Signal_4 | Signal_5 | Signal_6 |
|---|---|---|---|---|---|---|
| 1 | -0.63 | 0.01 | -1.16 | -1.36 | -0.55 | -1.54 |
| 2 | -1.26 | -0.65 | -1.35 | -1.15 | -1.01 | -1.32 |
| 3 | -1.90 | -1.51 | -1.49 | -0.84 | -1.33 | -1.03 |
| 4 | -2.23 | -1.62 | -1.32 | -0.52 | -1.66 | -0.80 |
| 5 | -2.34 | -1.33 | -1.06 | -0.23 | -1.92 | -0.63 |
| 6 | -2.46 | -1.45 | -1.04 | 0.04 | -1.65 | -0.67 |
| 7 | -1.94 | -1.13 | -0.62 | 0.35 | -1.27 | -0.34 |
| 8 | -1.62 | -0.89 | -0.73 | 0.64 | -1.04 | -0.10 |
| 9 | -1.50 | -0.84 | -0.42 | 0.90 | -0.72 | 0.15 |
| 10 | -0.86 | -0.43 | -0.37 | 1.14 | -0.26 | 0.34 |
| 11 | -0.82 | -0.33 | 0.09 | 1.31 | -0.02 | 0.53 |
| 12 | -0.14 | 0.13 | 0.39 | 1.45 | 0.35 | 0.72 |
| 13 | 0.19 | 0.20 | 0.62 | 1.51 | 0.70 | 0.89 |
| 14 | 0.88 | 0.72 | 0.90 | 1.48 | 1.01 | 1.02 |
| 15 | 1.40 | 1.06 | 0.97 | 1.38 | 1.34 | 1.10 |
| 16 | 1.79 | 1.11 | 1.33 | 1.21 | 1.56 | 1.19 |
| 17 | 2.36 | 1.52 | 1.44 | 0.98 | 1.85 | 1.28 |
| 18 | 2.33 | 1.39 | 1.68 | 0.69 | 1.65 | 1.35 |
| 19 | 2.66 | 1.51 | 1.87 | 0.40 | 1.97 | 1.43 |
| 20 | 2.86 | 1.62 | 2.05 | 0.13 | 2.12 | 1.49 |
Save this file as ica_mixed_signals.csv
✅ Python Code
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import FastICA
import warnings
# Optional: Ignore convergence warnings for cleaner output (you can comment this if you prefer to see them)
from sklearn.exceptions import ConvergenceWarning
warnings.filterwarnings("ignore", category=ConvergenceWarning)
# Step 1: Load the dataset
df = pd.read_csv("ica_mixed_signals.csv")
X = df.drop(columns=["Sample"])
# Step 2: Apply ICA with increased max_iter and a looser tolerance
ica = FastICA(n_components=6, random_state=42, max_iter=2000, tol=0.01)
recovered = ica.fit_transform(X)
# Step 3: Plot original (mixed) vs recovered (independent) signals
plt.figure(figsize=(14, 10))
for i in range(6):
# Left: Mixed signals
plt.subplot(6, 2, 2*i + 1)
plt.plot(X.iloc[:, i], linewidth=1.2)
plt.title(f"Mixed Signal {i+1}")
# Right: Recovered signals
plt.subplot(6, 2, 2*i + 2)
plt.plot(recovered[:, i], linewidth=1.2)
plt.title(f"Recovered Signal {i+1} (ICA)")
plt.tight_layout()
plt.suptitle("Signal Separation Using ICA", fontsize=16, y=1.02)
plt.show()
📊 Result:
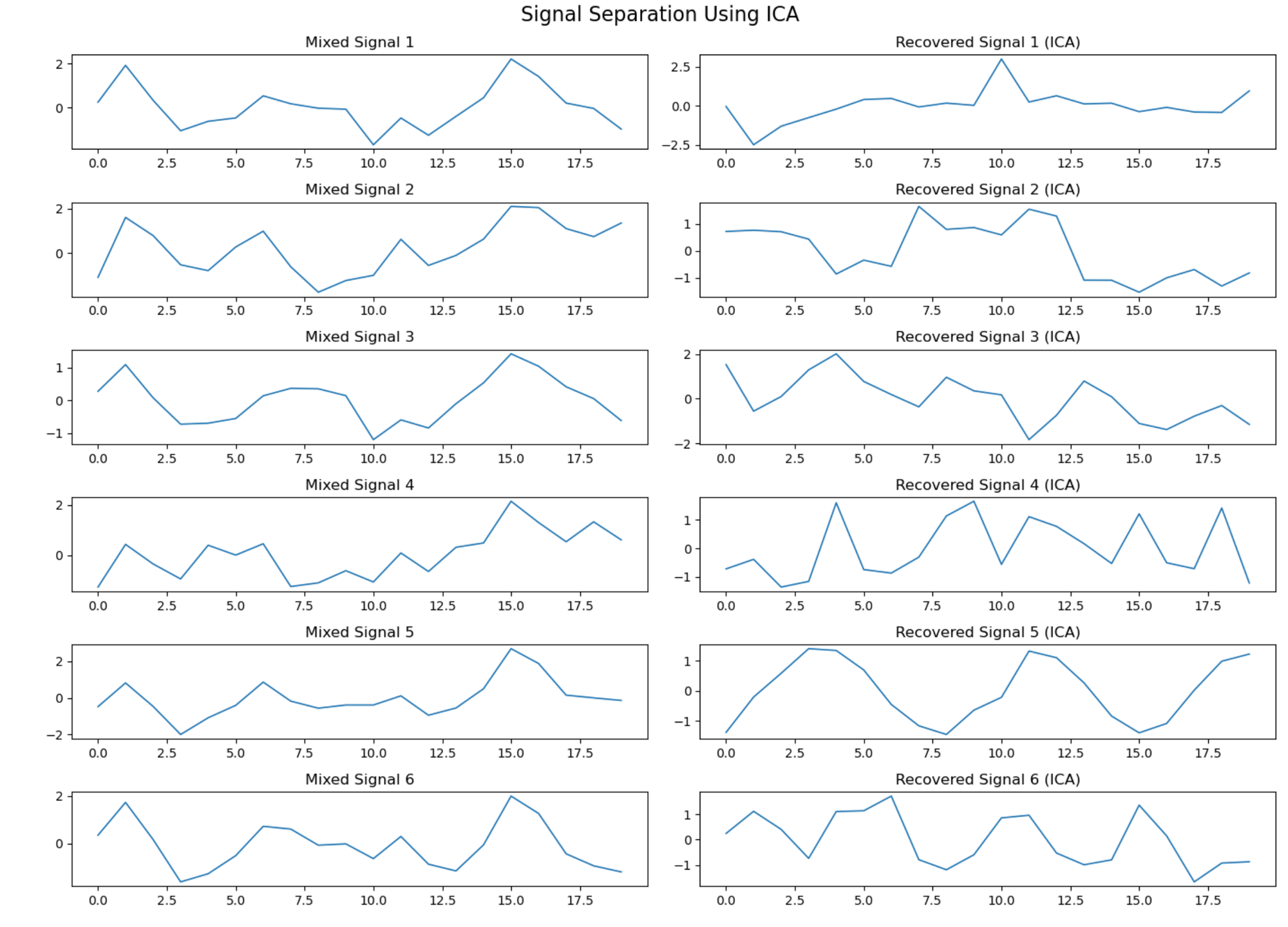
📊 What the Result Tells You
- Left plots = observed mixed signals (like tangled wires)
- Right plots = separated, independent signals (like detangled originals)
- ICA successfully recovers hidden sources, letting you interpret each independently
- This can clean your data, improve models, and reveal unseen patterns
🧠 What Does the Recovered Signal Represent in ICA?
The recovered signals are not simply denoised or cleaned versions of the mixed signals — they are entirely new signals that ICA believes to be the original, independent sources that were mixed to create your observed data.
In other words:
ICA doesn't "clean" the data — it unmixes it.
✅ The Recovered Signals Are:
- Statistically independent (as far as ICA can find)
- Mathematically reconstructed so that when you mix them again, they’d closely approximate the observed signals
- Potentially more interpretable, especially if you believe your data is a mixture of independent real-world processes (e.g., brain signals, audio sources)
❌ The Recovered Signals Are NOT:
- Just "denoised" or "smoothed" versions of the original
- Guaranteed to look cleaner or simpler — in fact, they might look more raw, sharp, or unexpected
- Ordered in any meaningful way (ICA doesn’t rank them like PCA does)
🤔 So… Are ICA Signals “Better”?
If your goal is:
| Goal | Use ICA? | Why |
|---|---|---|
| ✅ Separate hidden sources | Yes | ICA is perfect for this |
| ✅ Remove overlapping effects (like brain vs eye signals) | Yes | It separates them |
| ❌ Just reduce noise / smooth data | No | Try filters, PCA, or denoising autoencoders instead |
| ❌ Dimensionality reduction (compression) | Not really | PCA/VAE are better for that |
✅ Final Verdict
- Recovered signals = potential true sources
- Cleaner? Maybe. Better? Depends on your goal.
- ICA is for understanding & isolating signal sources, not for smoothing noise
💡 Nutshell
✅ ICA is essential when your data is a mixture of independent causes
✅ It helps recover structure, filter noise, and reveal hidden patterns
✅ Super powerful for bio-signals, finance, audio, sensors, and diagnostics
✅ Think of it as PCA’s smarter cousin — it doesn't just reduce, it separates!

💬 Join the DecodeAI WhatsApp Channel for regular AI updates → Click here